Formal Concept Analysis with Rust (2) - Basic Algorithm
在上一篇文章里, 我们介绍了Formal Concept的基本概念,概括起来就是对于一个文章-单词的集合\(D=\{d_1, d_2, \dots, d_n\}, W=\{w_1, w_2, \dots, w_m\}\),有:
- 对于任何一个文章的集合\(D_n = \{d_{i_1}, \dots, d_{i_2}\}\), 我们总可以用Closure操作把它变成一个合理的,极大的Formal Concept。即:对于\(D_n\)我们先寻找这些文章的共通单词的集合\(D_n^{\downarrow}\), 再通过这个单词的集合去寻找包含这些单词的文章集合\({D_n^{\downarrow\uparrow}}\),最终得到的文章-单词组合\(\{D_n^{\downarrow\uparrow}, D_n^{\downarrow}\}\)就是一个极大的Formal Concept。这个寻找共通单词,共通文章的操作就是Closure。在本文里,我们会把寻找共同单词的操作写成\(\downarrow\), 寻找共通文章则是\(\uparrow\), 因此一个Closure操作就是\(\downarrow\uparrow\).
- 根据上面的特性,我们显然从一个空集合\(\emptyset\)开始,向里面不停的添加文章,然后用Closure计算每次的极大Formal Concept,就可以最终得到所有的Formal Concept。 但这样得到的Formal Concept显然是会重复的,因此我们还要去掉重复生成的部分。显然,采用深度探索单纯的计算全部之后去重是一个最直接但最低效的做法。
在这一篇文章里,我们会根据
Parallel Recursive Algorithm for FCA, Petr Krajca, Jan Outrata and Vilem Vychodil, The International Conference on Concept Lattices and Their Applications, 2008.
里面的描述,实现一个单线程的Formal Concept列举算法。
Basic Representation
在实现算法之前,让我们先来考虑如何表示一个Formal Concept。从上面的总结里就可以看出,Closure算法需要大量的集合操作,因此我们选择使用一个数字来表示一篇文章或者一个单词,而一个Bit Vector则能够表示一个文章、单词的集合。用Rust的代码来说,定义是这样的:
struct FormalConcept {
extent: BitVec,
intent: BitVec,
}
struct FormalConceptLattice<T, K> {
object_map: HashMap<usize, T>,
attribute_map: HashMap<usize, K>,
concepts: Vec<FormalConcept>,
}
struct Relation {
row: HashMap<usize, BitVec>,
col: HashMap<usize, BitVec>,
}
这里,一个FormalConcept包含了extent(文章的集合)以及一个intent(单词的集合),这些文章和单词均用数字来表示,而它们实际的内容则保存在FormalConceptLattice的object_map和attribute_map里,在列举过程中我们并不需要实际的内容,因此这两个Map仅仅在输出的时候有用处。
在上一篇文章里我们已经提到,一个记录文章-单词关系的表通常是这样的
| doc\word | word1 | word2 | word3 | word 4 | ... |
|---|---|---|---|---|---|
| doc1 | 0 | 1 | 1 | 0 | ... |
| doc2 | 1 | 1 | 0 | 0 | ... |
| doc3 | 0 | 1 | 1 | 1 | ... |
| doc4 | 1 | 0 | 1 | 1 | ... |
| ... | ... | ... | ... | ... | .. |
Relation就是用来表示输入内容的,我们把每一行(文章)和每一列(单词)的01关系都单独记录下来,这样在计算过程中可以简单的使用它们而不必重复计算。
在Formal Concept的论文里,Tic-Tac-Toe,Mushroom等是常用的Dataset,不过在这篇文章里,我们使用下面的代码来生成随机的关系表作为数据:
// number of objects
let noo = 500;
// number of attributes
let noa = 50
// density
let p = 0.1
println!("{} {} {}", noo, noa, p);
let mut rng = rand::thread_rng();
for i in 0 .. noo {
print!("{} ", i);
for _ in 0 .. noa { print!("{} ", if rng.gen_range(0f32, 1f32) < p { 1 } else { 0 } ); }
println!("");
}
这里\(p\)是用来指定关系的密度,\(p\)越大,每个Object包含的Attribute就越多,当然Concept的数量也就越多,这个数量通常是爆发式增长的,如果\(p=1.0\)那么总是一个全列举问题,因此所有的Formal Concept列举算法的效率都会变得一样。
Closure Operation
下面我们先来实现Formal Concept里最重要的Closure操作:
// calculate extent -> intent operator
// input: a set of object
// output: a set of attributes which all objects share
// operation: calculate the intersection of attributes for all objects
fn down(r: &Relation, extent: &BitVec) -> BitVec {
assert_eq!(extent.len(), r.row.len());
extent
.iter()
.enumerate()
.fold(BitVec::from_elem(r.col.len(), true), |mut f0, (i, flag)| {
if flag {
f0.and(&r.row[&i]);
}
f0
})
}
// calculate intent -> extent operator
// input: a set of attributes
// output: a set of objects containing all input attributes
// operation: calculate the intersection of objects for all attributes
fn up(r: &Relation, intent: &BitVec) -> BitVec {
assert_eq!(intent.len(), r.col.len());
intent
.iter()
.enumerate()
.fold(BitVec::from_elem(r.row.len(), true), |mut f0, (i, flag)| {
if flag {
f0.and(&r.col[&i]);
}
f0
})
}
fn closure(r: &Relation, extent: &BitVec) -> FormalConcept {
let attributes = down(r, extent);
let objects = up(r, &attributes);
FormalConcept {
extent: objects,
intent: attributes,
}
}
这里首先实现了之前提到的\(\uparrow\)(up)和\(\downarrow\)(down)操作。对于up操作,给定一组Object,由于Relation里已经包含了每一行的信息,它们共通的单词显然就是全部集合的Intersection操作。这个操作每一次Closure操作都会发生数次,而选用BitVector正是因为这个——通常一个普通的集合,比如collections::HashSet都是用数列直接记录已经存在的数字,进行Intersection时对这些数字进行比较的算法总是\(O(min(|Self|, |Other|))\)的,当集合包含很多元素时,这个操作很耗时间。BitVector总是用Bit的位置来表示数字是否存在,因此对于总元素数为\(N\)的集合,它的长度是\(N/8\) bytes。更重要的是,BitVector之间的集合运算并不需要比较/删除操作,而是简单的比特运算就足够了—— Intersection是and,Union则是or。这能够极大的提高Closure的运算速度。
对于下面的例子:
| example data | att1 | att2 | att3 | att4 | att5 | att6 | att7 |
|---|---|---|---|---|---|---|---|
| obj1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| obj2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| obj3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| obj4 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
我们对Closure给一个输入 \(Intend = \{obj1\}\),
let mut initial_extent= BitVec::from_elem(4, false);
initial_extent.set(0, true);
let test_concept = closure(&relation, &initial_extent);
println!("{:?}", &test_concept)
可以得到下面的结果:
FormalConcept { extent: 1100, intent: 1010000 }
对于obj1,我们可以找的attribute的集合为\(\{att1, att2\}\), 根据这个集合可以得到一组object为\(\{obj1, obj2\}\),所以上面的计算给出了正确的结果。
Formal Concept Enumeration
下面我们就可以用Closure来进行Formal Concept的枚举了。我们首先把intent的集合设为包含所有的attributes \(B=\{w_1, \dots, w_m\}\),然后从\(\{B^{\uparrow},B^{\uparrow\downarrow}\}\)开始列举,每一次我们都向extent里面添加一个新的object。(事实上,intent和extent互换并不影响结果,因此不论从空集还是全集出发都能得到Formal Concept Lattice)
这个算法是这样的:
Function Enumerate(Concept {A, B}, current index j):
1. if B is already maximal, exit
2. for i in j .. number of object
2.1 if B already contains object i, continue
2.2 New Concept {C, D} = Closure(Concept {A, B})
2.3 if D[0 .. i] != B[0 .. i], continue
2.4 Run Enumerate(Concept{C, D}, i+1)
用图表示出来就是这样:
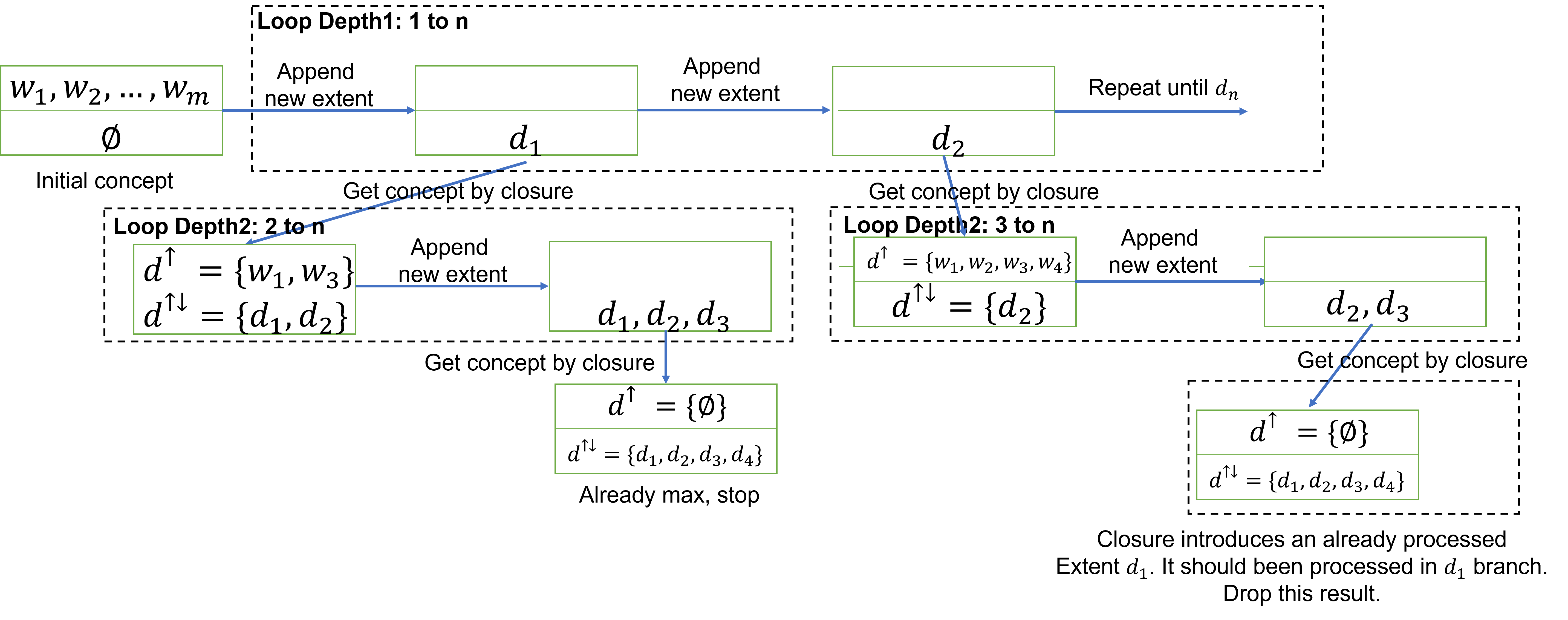
首先让我们来看一看基本的Depth-first Search的算法:
每一步中,给定一个Concept,和已经添加过的extent的index j,我们对当前Concept依次添加\(d_j, d_{j+1}, \dots\),然后对每一个Concept进行递归。
具体来说,在Extent是\(\emptyset\)时,我们首先每次添加一个Extent,比如第一次添加的是\(d_1\)。之后我们可以对这个添加之后的Extent进行closure操作来计算真正的Concept,在这里我们得到了\(\{(w_1, w_3), (d_1,d_2)\}\),可以看到在计算Concept之后,这个Extent并不是我们最初给定的那个Extent了。对于这个Extent,由于这是我们添加\(d_1\)之后的来的结果,它必定包含\(d_1\)。(对于第\(n\)此操作来说,由于我们之前添加了\(d_1 \cdots d_n\),所以它必定包含这些extent)因此,对于这个新的Concept,我们从\(d_2\)开始添加,不过由于\(d_2\)已经自然生成了,因此这里我们跳过它,添加\(d_3\)。而添加之后得到的结果是\(\{(\emptyset),(d_1,d_2,d_3,d_4)\}\),即已经最大了,所以可以停止这个分支。
而对于添加\(d_2\)的分支,可以看到我们再次添加\(d_3\)时,同样得到了一个\(\{(\emptyset),(d_1,d_2,d_3,d_4)\}\),但这里的结果跟之前时重复的,因此不应该输出。判断重复的方法则很简答:
对于一个新生成的Concept,它只能引入我们刚刚添加的extent之后的extent。如果它引入了一个之前的extent,我们显然已经在前面的分支里考虑过了,因此这个结果一定时重复的。
因此,对于这个\(d_2, d_3\)的分支,它计算之后多出了一个\(d_1\),但包含\(d_1\)的情况在我们添加\(d_1\)的分支里已经处理过了,因此这个结果总是重复的。
需要注意的是,这篇文章里我们用的是一个简化版的算法,这个算法并不保证Concept的顺序,如果你需要保证生成顺序,那么可以参考下面的文章:
Kuznetsov S.: Learning of Simple Conceptual Graphs from Positive and Negative Examples. PKDD 1999, pp. 384–391.
理解了上面的内容之后,我们就能把它写成代码了:
fn enumerate_fc(cur_concept: &FormalConcept, cur_obj: usize, r: &Relation) {
println!("{}", cur_concept);
if cur_concept.extent.all() {
return;
}
for obj in cur_obj..r.row.len() {
if !cur_concept.extent.get(obj).unwrap_or(false) {
let mut extent = cur_concept.extent.clone();
extent.set(obj, true);
let concept = closure(r, &extent);
// mask: 11111111111111111 00000000000
// ----------------- -----------
// 0 ... cur_obj-1 cur_obj ...
let mask = BitVec::from_fn(r.row.len(), |i| if i < obj { true } else { false });
let mut cur_left = cur_concept.extent.clone();
cur_left.and(&mask);
let mut new_left = concept.extent.clone();
new_left.and(&mask);
if cur_left == new_left {
// new concept generated
enumerate_fc(&concept, obj + 1, r);
}
}
}
}
上面的代码中生成了一个Mask,因为算法要求比较前N个数字的集合是否相同,而这次使用的BitVector库bit-vec并没有提供这个功能,才有了这个做法,但这么做实际上平白无故的多做了一次and。显然,理想的做法是直接比较BitVector的前N位——比如内部是用u8来储存的话,只需要比较前(cur_obj-1)/8byte以及(cur_obj-1)%8的Bit就足够了。
让我们初始化一个Concept,然后对上面的测试例子执行一下:
let initial_intent = BitVec::from_elem(relation.col.len(), true);
let initial_extent = up(&relation, &initial_intent);
let initial_concept = FormalConcept {
extent: initial_extent,
intent: initial_intent,
};
enumerate_fc(&initial_concept, 0, &relation);
可以得到:
read data: 134.3µs
construct initial concept: 239.1µs
enumerate: 167.5µs
0000 1111111
1100 1010000
1111 0000000
0100 1111000
0101 0100000
0010 0000011
0011 0000001
0001 0100101
可以看到,我们得到了所有的Formal Concept。
不过, 这个简单的算法的速度并不是很理想,比如对于3000 object, 50 attributes, \(p=0.1\)的数据来说,它的速度是:(release编译,不输出concept的内容)
read data: 20.7916ms
construct initial concept: 216.2µs
enumerate: 457.6723555s
实际上,同样50 attributes, \(p=0.1\)的情况下,执行时间和object数量的关系:
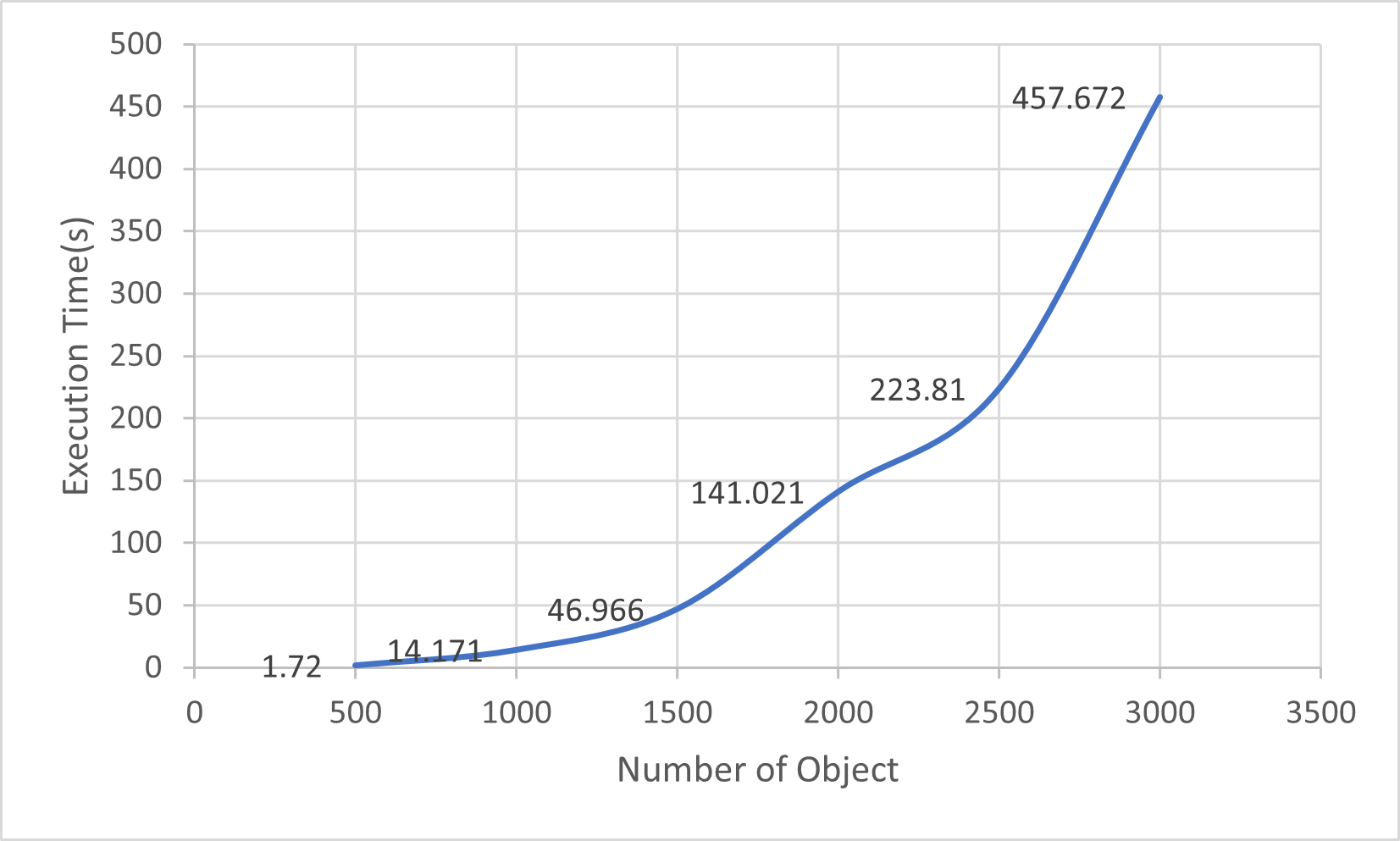
可以看到时间是指数式增长的,在5000 object的情况下,已经需要数十分钟来执行了。
Conclusion
在这篇文章里,我们简单描述了如何去计算一个Formal Concept Lattice。不过,由于算法并没有进行特别聪明的剪枝,速度上面并没有想象的那么理想。在下一篇文章里,我们将会对上面的算法并行化,提高它的执行速度。